viernes, 20 de noviembre de 2015
jueves, 19 de noviembre de 2015
miércoles, 18 de noviembre de 2015
"Principios de Huygens"
"Principios de Huygens"
Frentes de onda
A finales del siglo XVII, momento en el que la teoría más aceptada sobre la luz era la teoría corpuscular de Newton, el físico, matemático y astrónomo holandés Christian Huygens (1629-1695) propuso su hipótesis de que la luz era un fenómeno ondulatorio, de naturaleza casi igual a la del sonido. Enunció el llamado principio de Huygens, basado en el concepto de frente de onda.
Un frente de onda puede definirse como el lugar geométrico en que determinados puntos del medio en el que se propaga una onda (aire, agua…) son alcanzados en un mismo instante por dicha onda. Es por ello que todos los puntos que forman un frente de onda tienen la misma fase, es decir, están en la misma situación instantánea en el ciclo periódico de la onda. En la siguiente imagen vemos una representación de varios frentes de onda.
El principio de Huygens permite predecir la posición futura de un frente de onda cuando se conoce su posición anterior. Establece que los frentes de onda están formados por frentes de onda más pequeños, es decir, que cada punto de un frente de ondas primario se comporta como un emisor de ondas secundarias. Estas ondas secundarias son esféricas, tienen la misma frecuencia y se propagan en todas las direcciones con la misma velocidad que la onda primaria en cada punto. La envolvente de todas esas ondas secundarias es el nuevo frente de onda formado.
El principio de Huygens explica perfectamente la reflexión y refracción de la luz (también fácilmente explicables por la teoría corpuscular de Newton), así como los fenómenos ondulatorios que presenta, esto es, la difracción y las interferencias (hablaremos de difracción e interferencias en un futur post).
Segunda Ley De Newton "Teoría De La Luz"
"Teoría De La Luz"
Entre 1670 y 1672, Isaac Newton, trabajó intensamente en distintos problemas que estaban relacionados con la óptica.
Así realizo un conocido experimento, con prismas de vidrio transparentes, con caras no paralelas donde ocurre una doble refracción. En primera instancia, utilizó solo un prisma.Ubicó el prisma en un cuarto oscuro, en el cual entra un haz de luz blanca y atraviesa un trozo de cristal con caras planas, que no son paralelas. Al entrar y salir de este, la luz sufre una doble refracción. La luz se recoge en una pantalla, y lo que se obtiene es un haz que tiene todos los colores naturales del arcoiris separados, el rojo,naranja, verde, azul, añil y violeta.Entre 1670 y 1672, Isaac Newton, trabajó intensamente en distintos problemas que estaban relacionados con la óptica.
Así realizo un conocido experimento, con prismas de vidrio transparentes, con caras no paralelas donde ocurre una doble refracción. En primera instancia, utilizó solo un prisma.Ubicó el prisma en un cuarto oscuro, en el cual entra un haz de luz blanca y atraviesa un trozo de cristal con caras planas, que no son paralelas. Al entrar y salir de este, la luz sufre una doble refracción. La luz se recoge en una pantalla, y lo que se obtiene es un haz que tiene todos los colores naturales del arcoiris separados, el rojo,naranja, verde, azul, añil y violeta.
Algunos científicos de la misma época de newton afirmaban que el color se formaba en el prisma, pero el no creía estas afirmaciones, suponiendo que la luz blanca era una mezcla de haces de los siete colores del arcoiris. Según él, cada haz posee un grado propio y diferente de refracción en el prisma o vidrio. Esta hipótesis explica la formación del arco iris en la naturaleza, diciendo que la luz se refracta en las gotas de lluvia, separándose en forma similar a la del prisma.
Newton, para tratar de demostrar su hipótesis, hizo dos experimentos mas:
El primero consistió en añadir otro prisma, en forma invertida, con lo que concluyó que el has de luz se vuelve a unir para formar otra vez la luz blanca, igual como se ve en la siguiente imagen:
"La luz descompuesta en el primer prisma, se vuelve a juntar en el segundo invertido, para formar el haz de luz blanco de nuevo".
El "Disco de Newton", es el segundo experimento. Es un disco o ruleta que está dividida en siete partes, las cuales estan pintadas con un color del arcoiris distinto. Al girar este, a gran velocidad, la apariencia de la ruleta es blanca.
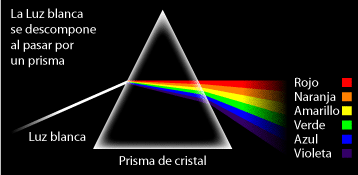
viernes, 13 de noviembre de 2015
"Video Final de la Semana"
Después de una semana muy atareada y de el examen entregamos el trabajo final de la semana....
jueves, 12 de noviembre de 2015
miércoles, 11 de noviembre de 2015
"Movimiento rectilíneo y rectilíneo uniformemente acelerado"
Los movimientos rectilíneos, que siguen una línea recta, son los movimientos más sencillos. Movimientos más complicados pueden ser estudiados como la composición de movimientos rectilíneos elementales. Tal es el caso, por ejemplo, de los movimientos de proyectiles.
El movimiento rectilíneo puede expresarse o presentarse como
Movimiento rectilíneo uniforme, o como
Movimiento rectilíneo uniformemente acelerado.
Este último puede, a su vez, presentarse como de caída libre o de subida vertical.
Movimiento rectilíneo uniforme
El movimiento rectilíneo uniforme (MRU) fue definido, por primera vez, por Galileo en los siguientes términos: "Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómense como se tomen, resultan iguales entre sí", o, dicho de otro modo, es un movimiento de velocidad v constante.
El MRU se caracteriza por:
a) Movimiento que se realiza en una sola dirección en el eje horizontal.
b) Velocidad constante; implica magnitud, sentido y dirección inalterables.
c) La magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración = 0).
Concepto de rapidez y de velocidad
Muy fáciles de confundir, son usados a menudo como equivalentes para referirse a uno u otro.
Pero la rapidez (r) representa un valor numérico, una magnitud; por ejemplo, 30 km/h.
En cambio la velocidad representa un vector que incluye un valor numérico (30 Km/h) y que además posee un sentido y una dirección.
Cuando hablemos de rapidez habrá dos elementos muy importantes que considerar: la distancia (d) y el tiempo (t), íntimamente relacionados.
Así:
Si dos móviles demoran el mismo tiempo en recorrer distancias distintas, tiene mayor rapidez aquel que recorre la mayor de ellas.
Si dos móviles recorren la misma distancia en tiempos distintos, tiene mayor rapidez aquel que lo hace en menor tiempo.
Significado físico de la rapidez
La rapidez se calcula o se expresa en relación a la distancia recorrida en cierta unidad de tiempo y su fórmula general es la siguiente:
Como corolario, la distancia estará dada por la fórmula:Usamos v para representar la rapidez, la cual es igual al cociente entre la distancia (d) recorrida y el tiempo (t) empleado para hacerlo.
Según esta, la distancia recorrida por un móvil se obtiene de multiplicar su rapidez por el tiempo empleado.
A su vez, si se quiere calcular el tiempo empleado en recorrer cierta distancia usamos
El tiempo está dado por el cociente entre la distancia recorrida y la rapidez con que se hace.
Problemas o ejercicios sobre el movimiento rectilíneo uniforme:
Ejercicio 1
Un automóvil se desplaza con una rapidez de 30 m por segundo, con movimiento rectilíneo uniforme. Calcule la distancia que recorrerá en 12 segundos.
Analicemos los datos que nos dan:
Apliquemos la fórmula conocida:
y reemplacemos con los datos conocidos:
¿Qué hicimos? Para calcular la distancia (d), valor desconocido, multiplicamos la rapidez (v) por el tiempo (t), simplificamos la unidad segundos y nos queda el resultado final en metros recorridos en 12 segundos: 360 metros
Ejercicio 2
El automóvil de la figura se desplaza con movimiento rectilíneo uniforme ¿cuánto demorará en recorrer 258 kilómetros si se mueve con una rapidez de 86 kilómetros por hora?
Analicemos los datos que nos dan:
Apliquemos la fórmula conocida para calcular el tiempo:
y reemplacemos con los datos que tenemos:
¿Qué hicimos? Para calcular el tiempo (t), valor desconocido, dividimos la distancia (d) por la rapidez (v), simplificamos la unidad kilómetros y nos queda el resultado final en horas: 3 horas para recorrer 258 km con una rapidez de 86 km a la hora.
Ejercicio 3
¿Con qué rapidez se desplaza un móvil que recorre 774 metros en 59 segundos?
Analicemos los datos conocidos:
Aplicamos la fórmula conocida para calcular la rapidez:
¿Qué hicimos? Para calcular la rapidez (v), valor desconocido, dividimos la distancia (d) por el tiempo (t), y nos queda el resultado final: la rapidez del móvil para recorrer 774 metros en 59 segundos: 13,11 metros por segundo.
Ejercicio 4
Los dos automóviles de la figura parten desde un mismo punto, con movimiento rectilíneo uniforme. El amarillo (móvil A) se desplaza hacia el norte a 90 km por hora, y el rojo (móvil B), hacia el sur a 80 km por hora. Calcular la distancia que los separa al cabo de 2 horas.
Veamos los datos que tenemos:
Para el móvil A:
Para el móvil B:
Calculamos la distancia que recorre el móvil A:
Calculamos la distancia que recorre el móvil B:
Sumamos ambas distancias y nos da 340 km como la distancia que separa a ambos automóviles luego de 2 horas de marcha.
Ejercicio 5
El corredor de la figura trota de un extremo a otro de la pista en línea recta 300 m en 2,5 min., luego se devuelve y trota 100 m hacia el punto de partida en otro minuto.
Preguntas: ¿Cuál es la rapidez promedio del atleta al recorrer ambas distancias? ¿Cuál es la rapidez media del atleta al recorrer los 400 metros?
Veamos los datos que tenemos:
Para el primer tramo:
Calculamos su rapidez:
Para el segundo tramo:
Calculamos su rapidez:
Rapidez promedio:
La rapidez promedio del atleta fue de 110 metros por minuto.
Veamos ahora cuál fue la velocidad media (vm)para recorrer los 400 metros:
La rapidez media del atleta fue de 114,29 metros por minuto.
Ya vimos que el movimiento rectilíneo puede expresarse o presentarse como
Movimiento rectilíneo uniforme,
o como
Movimiento rectilíneo uniformemente acelerado.
Este último puede, a su vez, presentarse como de caída libre o de subida o tiro vertical.
El movimiento rectilíneo uniformemente aceleradoes un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.
Este es el significado del movimiento uniformemente acelerado, el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.
En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.
En este movimiento la velocidad es variable, nunca permanece constante; lo que si es constante es la aceleración.
Entenderemos como aceleración la variación de la velocidad con respecto al tiempo. Pudiendo ser este cambio en la magnitud (rapidez), en la dirección o en ambos.
Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:
Velocidad inicial Vo (m/s)
Velocidad final Vf (m/s)
Aceleración a (m/s2)
Tiempo t (s)
Distancia d (m)
Para efectuar cálculos que permitan resolver problemas usaremos las siguientes fórmulas:
Consejos o datos para resolver problemas:
La primera condición será obtener los valores numéricos de tres de las cinco variables. Definir la ecuación que refleje esas tres variables. Despejar y resolver numéricamente la variable desconocida.
Tener cuidado con que en algunas ocasiones un dato puede venir disfrazado; por ejemplo:
"un móvil que parte del reposo.....", significa que su velocidad inicial es Vo = 0 ; "en una prueba de frenado...", significa que su velocidad final es Vf = 0.
Veamos un problema como ejemplo
En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s2. ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?
Veamos los datos que tenemos:
Conocemos tres de las cinco variables, entonces, apliquemos las fórmulas:
Averigüemos primero la distancia que recorrerá durante los 20 segundos:
Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:
Respuestas:
Si nuestro tren, que viaja a 16 m/s, es acelerado a 2 m/s recorrerá 720 metros durante 20 segundos y alcanzará una velocidad de 56 m/s.
Movimiento rectilíneo uniformemente retardado
En los movimientos uniformemente decelerados o retardados la velocidad disminuye con el tiempo a ritmo constante. Están, pues, dotados de una aceleración que aunque negativa es constante. De ahí que todas las fórmulas usadas para los movimientos uniformemente acelerados sirvan para describir los movimientos uniformemente retardados, considerando sólo que su signo es negativo.
Por lo tanto, para efectuar cálculos que permitan resolver problemas que involucren aceleración negativa o deceleración, usaremos las siguientes fórmulas:
martes, 10 de noviembre de 2015
Momento de un par de fuerzas
Un par de fuerzas es un sistema de dos fuerzas paralelas, de igual intensidad y de sentido contrario, que produce un movimiento de rotación.
Cuando alguien utiliza una llave para quitar la rueda de un coche (automóvil), aplica dos fuerzas iguales y de sentido contrario.
Se observa que la llave no experimenta movimiento de traslación alguno, es decir, no se desplaza, pero sí gira bajo la acción del par de fuerzas.
Aunque la resultante de las fuerzas del par es nula (R = F1 – F2 = 0), sin embargo, los momentos de cada fuerza del par, con respecto al punto E, suman su capacidad de producir un giro, por ello el efecto de un par de fuerzas es producir una rotación.
El volante (manubrio) de un carro (automóvil) es una aplicación práctica de un par de fuerzas.
También lo son las regaderas que se usan en los jardines para regar el césped.
Entonces, diremos que un par de fuerzas, es un sistema formado por dos fuerzas de la misma intensidad o módulo, pero de dirección contraria, capaces de producir en su momento una rotación.Entonces, un par de fuerzas queda caracterizado por su momento (M).
El valor del momento de un par de fuerzas es igual al producto de una de las fuerzas por la distancia que las separa:
Esto es,
M = F1d = F2d
La distancia que separa las fuerzas recibe el nombre de brazo del par
Ejemplo: Calcular el valor del momento de un par de fuerzas cuya intensidad es 5N si el brazo del par mide 2 m.
Solución:
M = F • d = 5N • 2m = 10Nm
Ejemplos comunes de pares de fuerza
En nuestra vida cotidiana encontramos numerosos aparatos o realizamos movimiento que se hacen aplicando un par de fuerzas.
Entre otros tenemos:
Destornillador
Sacacorchos
Apertura o cierre de una llave (grifo)
Ajustador de brocas de un taladro.
Batidora manual
Volante de un vehículo
 |
| Utilizamos el sacacorchos, pero el trabajo lo realiza un par de fuerzas. |
Ejercicios.
Calcular el valor del momento de los siguientes pares de fuerzas:
1) 8N separadas 8m.
2) 5N separadas 10m.
3) 6N separadas 3m.
4) 12N separadas 4m.
5) 10N separadas 6m.
6) 20N separadas 5m.
7) 9N separadas 6m.
8) 7N separadas 3m.
 |
| Un par de fuerzas produce un movimiento de rotación, |
viernes, 6 de noviembre de 2015
"Tema Expuesto en Clase (PRIMERA CONDICIÓN DE EQUILIBRIO)"
PRIMERA LEY DE NEWTON (CONDICIÓN DE EQUILIBRIO)
Un cuerpo se encuentra en estado de equilibrio traslacional si y sólo si la suma vectorial de las fuerzas que actúan sobre él es igual a cero.
Cuando un cuerpo está en equilibrio, la resultante de todas las fuerzas que actúan sobre él es cero. En este caso, Rx como Ry debe ser cero; es la condición para que un cuerpo esté en equilibrio:
EJEMPLO:
Una pelota de 300N cuelga atada a otras dos cuerdas, como se observa en la figura. Encuentre las tensiones en las cuerdas A, B Y C.
SOLUCIÓN:
El primer paso es construir un diagrama de cuerpo libre:
Al sumar las fuerzas a lo largo del eje X obtenemos :
Fx = -A cos 60° + B cos 40° = 0
Al simplificarse por sustitución de funciones trigonométricas conocidas tenemos:
(Ecuación 1) -0.5A + 0.7660B = 0
Obtenemos una segunda ecuación sumando las fuerzas a lo largo del eje Y, por lo tanto tenemos:
(Cos 30° + cos 50° )
( Ecuación 2) 0.8660A + 0 .6427B = 300N
En las ecuaciones 1 y 2 se resuelven como simultanea A y B mediante el proceso de sustitución. Si despejamos A tenemos:
A = 0.7660 / 0.5
A = 1.532B
Ahora vamos a sustituir esta igualdad en la ecuación 2
0.8660(1.532B) + 0.6427B = 300N
Para B tenemos:
1.3267B + 0.6427B = 300N
1.9694B = 300N
B= 300N / 1.9694B= 152.33N
Para calcular la tensión en A sustituimos B = 152.33 N
A = 1.532(152.33N) = 233.3N
La tensión en la cuerda C es 300N , puesto que debe ser igual al peso.
jueves, 5 de noviembre de 2015
miércoles, 4 de noviembre de 2015
"Componentes Rectangulares De La Fuerza"
COMPONENTES RECTANGULARES DE LA FUERZA
Considerando la fuerza F que actúa en el origen. Para definir la dirección de F se traza el plano vertical OBAC que contiene a F. Este plano pasa a través del eje vertical y , su orientación esta definida por el ángulo φ que forma con el plano xy, mientras que la dirección de F dentro del plano esta definido por el ángulo θy que forma F con el eje y.
La fuerza F puede descomponerse en una componente vertical Fy y un a componente horizontal Fh; esta operación se realiza en el plano OBAC de acuerdo con las reglas desarrolladas ya vistas. Las componentes escalares correspondientes son
Fy = | F | cos θy Fh = | F | sen θy La Fh
puede separarse en sus dos componentes rectangulares Fx y Fz a lo largo de los ejes x y z, respectivamente. Esta operación se realiza en el plano xz. De esta manera se obtienen las expresiones siguientes para las componentes escalares correspondientes:
Fx = | Fh | cos φ = | F | sen θy cos φ
Fy = | Fh | sen φ = | F | sen θy sen φ
Aplicando el teorema de Pitágoras a los triángulos OAB y OCD (se omiten cálculos) se obtiene la siguiente relación entre la magnitud de F y sus componentes rectangulares escalares
la relación que existe entre la fuerza F y sus tres componentes Fx, Fy, y Fz se presenta más fácil si se
observa lo siguiente
Con el uso de los vectores unitarios i, j y k dirigidos a lo largo de los ejes x, y y z respectivamente se
obtienen las componentes rectangulares de la fuerza:
Fx = | F | cos θx i Fy = | F | cos θy j Fz = | F | cos θz k
Conformando así la expresión vectorial de la fuerza:
F = F x i + F y j + F z k
finalmente:
F = | F | cos θx i + | F | cos θy j + | F | cos θz k
F = | F | (cos θx i + cos θy j + cos θz
k )
F = | F | ef
donde ef = cos θx i + cos θy j + cos θz k
Ejemplo:
Si F = 500 N forma ángulos de 600
, 450
y 1200
con los ejes x, y y z
respectivamente. Encuentre las componentes Fx Fy y Fz de la fuerza.
Componentes esclares:
Fx = F cos θx = 500 cos 60 = 250 N
Fy = F cos θy = 500 cos 45 = 353.55 N
Fz = F cos θz = 500 cos 120 = - 250 N
Componentes rectangulares
Fx = F cos θx i = 500 cos 60 = 250 N
Fy = F cos θy j = 500 cos 45 = 353.55 N
Fz = F cos θz k = 500 cos 120 = - 250 N
Expresión vectorial
F= 250 i + 353.55 j – 250 k [ N ]
Ejemplo:
Una fuerza F tiene las componentes F x = 20 lb, F y = - 30 lb y Fz = 60 lb.
Determine la magnitud de F y los ángulos θx , θy y θz que forma con los ejes
coordenados.
Ejemplo:
El alambre de una torre está anclado en A por medio de un perno. La tensión en el
alambre es de 2500 N. Determine a) las componentes Fx , Fy y Fz de la fuerza que
actúa sobre el perno y b) los ángulos θx , θy y θz que definen la dirección de la
fuerza
Ejemplo:
sección de una pared de concreto precolado se sostiene temporalmente por los
cables mostrados. Se sabe que la tensión es de 840 lb en el cable AB y 1200 lb en
el cable AC, determine la magnitud y la dirección de la resultante de las fuerzas
ejercidas por los cables AB y AC sobre la estaca A.
martes, 3 de noviembre de 2015
"Las fuerzas coplanares"
Se encuentran en un mismo plano y en 2 ejes, a diferencia de las no coplanares que se encuentran en mas de un plano, es decir en 3 ejes. Tienen dos condiciones independientes algebraicas de equilibrio. Pueden expresarse en tres formas:
1.- ∑Fx = ∑Fy = 0 ------> la suma algebraica de los componentes según los ejes x, y (en el plano de las fuerzas) es cero.
2.- ∑Fx = ∑Ma = 0 -----> la suma algebraica de las componentes según cualquier eje y la suma algebraica de los momentos de todas las fuerzas respecto a un punto es cero (el punto debe estar en el plano de las fuerzas y la línea que lo une en la intersección de las fuerzas, debe ser inclinado al eje tomado).
3.- ∑Ma = ∑Mb = 0 -----> En esta forma se explica, asimismo, refiriéndose a momentos respecto dos puntos no colineales con la intersección aludida.
"Hola Mundo"
Nosotros somos un equipo de "Ingenieros en Sistemas Computacionales", del ICEP Colima, y en este Blog daremos a conocer diversos temas sobre la Materia de Física, de los cuales daremos Información detallada, vídeos y algunos Experimentos.
Suscribirse a:
Entradas (Atom)